Na ostatnią część zajęć zostali po opieką pani Beaty Florczak uczniowie klas V. Wszyscy uczniowie otrzymali następujące zadania do rozwiązania w domu:

DZIENNIKARZ

30.10.2014r. odbyły się kolejne zajęcia z zaproszonym gościem – p. Dariuszem Koźlenko, z zawodu dziennikarzem. Pan Dariusz pracował w wielu gazetach- był jednym z założycieli „Życia Pabianic”, pracował w „Super Expressie”, tygodnikach „Newsweek”, „Polityka”. Opowiedział o swoich ciekawych reportażach podróżniczych, np. w Himalaje, o spływie rzekami na trasie Warszawa – Berlin, o cyklu artykułów nt. sportów ekstremalnych, miejsc, które zostały dotknięte powodzią (Sandomierz), objętych wojną czy reportażach o zwykłych ludziach, którym poprzez swoje artykuły dziennikarze mogą pomóc. Mieliśmy możliwość obejrzenia zdjęć, albumów, tygodników, a w końcu wypróbować swoich możliwości dziennikarskich pisząc na starej maszynie do pisania.  Okazało się, że i w tym zawodzie ważna jest matematyka np. w liczeniu prędkości lotu, przeliczaniu odległości w terenie, zamianie jednostek czasu czy obliczeniach pieniężnych.

Na drugą część zajęć pozostali uczniowie klas IV, którzy po opieką pana Janusza Koźlenki rozwiązywali zadania matematyczne związane z pracą dziennikarza.

Uczniowie wszystkich klas otrzymali też zadania do rozwiązania w domu:

PIELĘGNIARKA

6.11.2014r. mieliśmy spotkanie z kolejnym gościem – była nim pielęgniarka,  pani Krystyna Kasprzak. W pierwszej słowach opowiedziała nam o ukończonej przez siebie szkole, czynnościach wykonywanych przez pielęgniarki w szpitalach, przychodniach, szkołach, a także o  cechach, jakie musi posiadać pielęgniarka, aby dobrze wykonywać swoją pracę. W prosty sposób zwróciła uwagę na przydatność matematyki również w jej zawodzie – przy przeliczaniu dawek leków, tworzeniu oraz odczytywaniu danych z siatek centylowych i liczeniu BMI. Później nastąpiło uproszczone badanie wzroku, mierzyliśmy sobie tętno. Ostatnim zadaniem z udziałem pani pielęgniarki było ważenie niektórych uczniów i ich plecaków. Dowiedzieliśmy się, że bezpieczny ciężar tornistra nie powinien przekraczać 10% wagi ucznia. Zaczęło się przeliczanie. Niestety, okazało się, że niektórzy noszą plecaki ważące nawet więcej niż 6 kg, to o wiele za dużo! Spróbujmy zastanowić się w domu, czy wszystkie rzeczy znajdujące się w plecaku są  nam potrzebne.  Ciężkie tornistry nadmiernie przeciążają kręgosłup i przyczyniają się do powstawania wad postawy, przede wszystkim skoliozy – bocznego skrzywienia kręgosłupa.

Na drugą część zajęć pozostali uczniowie klas VI, którzy po opieką pana Henryka Kurasiewicza rozwiązywali zadania matematyczne związane z pracą lekarza i pielęgniarki.

Uczniowie wszystkich klas otrzymali też zadania do rozwiązania w domu:

 

klasa VI

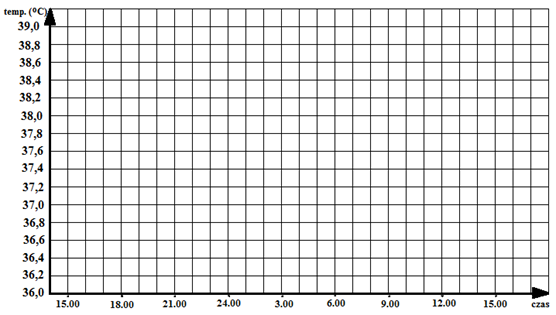
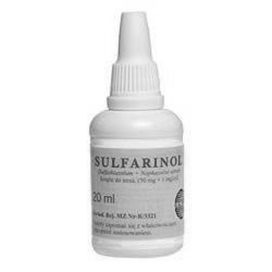
Zadanie 1 Mama notowała w tabeli, jak zmienia się temperatura ciała chorej córki. Przedstaw te wyniki w układzie współrzędnych. Zapisz dwie informacje, które można odczytać z wykresu.   godz. 14.00 16.30 20.00 23.00 6.45 11.00 13.30 16.15 temp. 37,4⁰C 38⁰C 38,5⁰C 37,8⁰C 39⁰C 38,3⁰C 37,6⁰C 36,9⁰C     Zadanie 2 Oto urywek ulotki leku.   Stosować zgodnie z zaleceniami lekarza.   Zazwyczaj stosowana dawka u dorosłych i dzieci powyżej 12 roku życia to 1-2 krople co 4-6 godzin do każdego otworu nosowego. Lek należy zakroplić do każdego otworu nosowego na skrzydełko nosa, następnie kilkakrotnie zacisnąć nos palcem wskazującym i kciukiem. Przed użyciem wstrząsnąć. Leku nie należy stosować dłużej niż przez 5 dni.   Ile mililitrów leku zastanie w buteleczce jeżeli zastosujemy minimalną dawkę leku (zgodnie z ulotką) przez pięć dni. Przyjmujemy, że jedna kropla to 0,1 ml. Zadanie 3 Według Światowej Organizacji Zdrowia ciężar tego, co dziecko dźwiga na plecach, nie powinien przekraczać 10. procent jego wagi.   6 listopada  podczas zajęć z zaproszonym gościem będziesz miał(a) możliwość poznać wagę swojego ciała. Zapamiętaj wynik i oblicz jakiej wagi nie powinien przekraczać twój tornister.   Waga mojego ciała . . . . . . . .   .     Waga mojego tornistra nie powinna przekraczać . . . . . . . . .   .   KRAWIEC   13.11.2014r. zawitała do nas mistrzyni igły – pani Urszula Masłowska. Pani Urszula jest nie tylko krawcową, ale i nauczycielką zawodu w szkole ponadgimnazjalnej, a przede wszystkim pasjonatką tego zawodu.  Opowiedziała o swojej pracy, o plusach i minusach swojego zawodu. Pokazała również potrzebne w pracy krawcowej narzędzia, w jaki sposób zdejmuje się miarę potrzebną do uszycia bluzki, spódnicy, spodni. Na koniec uczniowie mieli możliwość wykonania zadania w grupach  – należało według instrukcji skrócić o określoną długość przód spódnicy, wykrojony przez gościa, a następnie obliczyć, jakiej długości jest poprawiona spodniczka.              Na drugą część zajęć pozostali uczniowie klas V, którzy po opieką pana Janusza Koźlenki rozwiązywali zadania matematyczne związane z pracą krawcowej. Uczniowie wszystkich klas otrzymali też zadania do rozwiązania w domu: klasa IV klasa V   klasa VI   Zadanie 1 Krawcowa uszyła 4 poszewki. Do każdej przyszyła po tyle samo guzików. Zużyła 20 guzików. Po ile guzików przyszyła do jednej poszewki?   Zadanie 2 Krawiec zmierzył długość kuponu materiału. Stwierdził, że brakuje mu 4 cm do pełnych 3 metrów. Jaka jest długość kuponu?   Zadanie 3 Krawiec ma tkaninę o długości 40 m. Codziennie odcina kawałek o długości 5 m. W którym z kolei dniu odetnie ostatni kawałek tkaniny? Zadanie 1 Dwie krawcowe obszywają brzegi obrusów, pierwszej ta czynność zabiera 10 min, a drugiej 12 min, obie zaczynają pracę o 8.00. O której godzinie obydwie pierwszy raz skończą jednocześnie obszywać obrusy, ile razy skończą jednocześnie obszywać obrusy w ciągu ośmiogodzinnego dnia pracy?   Zadanie 2 Na uszycie garnituru krawiec potrzebuje ośmiometrowy kupon materiału. Na uszycie spodni zużyje  potrzebnego materiału, a na marynarkę pozostałą część. Ile metrów materiału krawiec zużyje na uszycie marynarki?   Zadanie 3 Dobry, damski krawiec w wielkiej, ciężkiej beli przyniósł piękny materiał i codziennie go dzielił. Metrów w beli trzydzieści, po 5 metrów odcina. W którym dniu raz ostatni dzieli się tkanina? Zadanie 1 Krawiec zapłacił 587,70 zł za materiały dwóch gatunków: po 21,60 zł i po 12,50 zł za 1 metr materiału. Ile metrów droższego materiału kupił krawiec, jeśli miał 9 metrów tańszego?   Zadanie 2 Jeśli do wieku krawca dodamy 9 i podzielimy całość przez 10 to otrzymamy najmniejszą wspólną wielokrotność liczb 2 i 3. Żona krawca jest od niego młodsza o 4 lata, zaś córka urodziła się, gdy krawiec miał 24 lata. Ile lat ma krawiec, ile lat ma jego żona, a ile lat ma jego córka?   Zadanie 3 Do wykonania modelowej serii sukienek zatrudniono 12 krawcowych na 25 dni. Ile krawcowych trzeba zatrudnić, aby praca była wykonana w czasie o 5 dni krótszym? FOTOGRAF   20.11.2014r. odwiedził nas zawodowy fotograf, pan Miłosz Piskorski. Fotograf opowiedział nam o swoim wykształceniu i pracy zawodowej – poza prowadzeniem zakładu fotograficznego pan Piskorski pracuje też w szkole ponadgimnazjalnej, w klasie fotograficznej.  Mogliśmy zobaczyć profesjonalny sprzęt fotograficzny, przykładowe zdjęcia wykonywane przez naszego gościa oraz zdjęcia na jego stronie internetowej. Oczywiście były tez nawiązania do matematyki i wykorzystania jej w zawodzie fotografa. Najciekawsze okazały się ćwiczenia praktyczne – tworzenie fotomontażu z przypadkowo dobranych elementów i fotografii oraz obrabianie wykonanej uczniom fotografii.     Na drugą część zajęć pozostali uczniowie klas VI, którzy po opieką pani Beaty Florczak rozwiązywali zadania matematyczne związane z pracą fotografa. Uczniowie wszystkich klas otrzymali też zadania do rozwiązania w domu: klasa IV klasa V   klasa VI   Zadanie 1 Popołudniowe zajęcia  fotograficzne Uczniowskiego Klubu „Fotka” trwają 2 godziny i 30 minut. O której godzinie  Natalka rozpoczęła te zajęcia, jeśli skończyła je o godzinie 18.45?   Zadanie 2 Rodzice z trójką dzieci wybrali się na wystawę fotograficzną.  Ich najmłodszy syn Pawełek ma 6 lat, średnia Ola jest o dwa lata od niego starsza, a najstarszy Krzyś jest od  Pawełka dwa razy starszy. Wiek Cena biletu Dzieci do lat 7 12zł Dzieci i młodzież szkolna 16zł Studenci 16zł Dorośli 18zł a)     Ile zapłaci za bilety  cała rodzina? b)     Ile zapłaciliby rodzice, idąc  na wystawę tylko z najstarszym synem? c)     Ile zapłaciłby studiujący wujek Oli,  zabierając ją na wystawę? d)     Ile zapłaciliby rodzice, kupując bilety tylko swoim dzieciom?   Zadanie 3 Rodzice Oli chcą kupić na raty dobry aparat fotograficzny, który kosztuje 1800zł. Przy odbiorze muszą wpłacić 180zł, a resztę kwoty będą  płacić  w 12 równych ratach. Jaka będzie  wysokość raty? Zadanie 1 W klasie Kuby jest 26 uczniów. Planują  obejrzenie wystawy fotograficznej, na którą bilet kosztuje 14zł. Zebrano już 350zł. Czy wszyscy uczniowie wpłacili  już za bilet?   Zadanie 2 Fotograf robiący zdjęcia uczniom w szkole  jednego dnia sprzedał połowę zdjęć, drugiego dnia połowę reszty i jeszcze  pozostało mu 27 zdjęć. Ile wszystkich zdjęć miał do sprzedania?  Ile zdjęć sprzedał fotograf w ciągu tych dwóch dni?   Zadanie 3 W hurtowni fotograficznej do pakowania aparatów używa się pudełek o wymiarach 280mm X 280mm X 110mm. Jaki będzie  koszt 100 pudełek, jeżeli producent  pobiera 3,5zł ma m2  kartonu, a na wykonanie uchwytów przeznacza dodatkowe 140cm2 kartonu?       Zadanie 1 Cenę profesjonalnego  aparatu fotograficznego obniżono o 400zł. Obniżka jest równa 2/5 wartości aparatu. a)       Oblicz cenę aparatu przed obniżką. b)       Oblicz nową cenę aparatu.   Zadanie 2 Zakład fotograficzny przesyła 1/5 pensji pana Kowalskiego do urzędu  skarbowego (jest to podatek od  wynagrodzenia). W tym miesiącu pensja pana Kowalskiego wynosiła 2480zł. Ile pieniędzy z tej pensji zakład przekaże do urzędu skarbowego? Ile pieniędzy  otrzyma pan Kowalski?   Zadanie 3 Pan Artur kupił aparat fotograficzny za 1000zł. Pozostało mu ponad 250zł. Ile pieniędzy mógł mieć pan Artur przed zrobieniem zakupów? Podaj kilka możliwości.       SPORTOWIEC   27.11.2014r. odwiedził nas kolejny zaproszony gość, sportowiec, p. Wojciech Woźniak. Zajęcia były bardzo ciekawe. Nasz gość opowiedział nam o różnych dyscyplinach sportowych – min. żeglarstwie, piłce nożnej, piłce siatkowej, biegach, skokach narciarskich, nordic walking,  pchnięciu kulą, golfie, wskazując na obecność matematyki w każdej z tych dziedzin. Poznaliśmy wymiary boisk do różnych gier sportowych,  budowę, wielkości i masy piłek do wybranych gier oraz wiele sportowych ciekawostek.  Przekazane informacje zostały wzbogacone o przygotowaną przez pana Woźniaka prezentację i pokaz wykorzystywanego na co dzień sprzętu sportowego.  Na koniec mieliśmy możliwość porównania ciężaru kuli i piłki lekarskiej oraz popróbować swoich sił w grze w mini golfa.   Na drugą część zajęć pozostali uczniowie klas V, którzy po opieką pana Henryka Kurasiewicza rozwiązywali zadania matematyczne związane ze sportem i sportowcami. Uczniowie wszystkich klas otrzymali też zadania do rozwiązania w domu: Kl. VI   1.      Kort tenisowy       Mecz tenisowy rozgrywany jest na prostokątnym korcie tenisowym. Długość kortu wynosi 23,77 m, a szerokość 10,97 m dla meczów deblowych. Pole powierzchni kortu do gry pojedynczej jest o 65,1298 m² mniejsze. Jaka jest szerokość kortu w grze pojedynczej? W obliczeniach możesz korzystać z kalkulatora.       2.      Oto fragment tabeli rundy zasadniczej w pewnym sezonie rozgrywek polskiej ligi hokeja na lodzie.   Msc. Zespół M Pkt W WPD WPK PPD PPK P 1 Sanok 42   29 2 1 0 0 10 2 Cracovia 42   25 0 3 1 0 13 3 Oświęcim 42   26 0 0 1 2 13 4 Jastrzębie 42   22 3 1 1 3 12 5                   6                     Msc. = lokata w tabeli, M = liczba rozegranych spotkań, Pkt = Liczba zdobytych punktów, W = Liczba meczów wygranych, WPD = Liczba meczów wygranych po dogrywce, WPK = Liczba meczów wygranych po karnych, PPD = Liczba meczów przegranych po dogrywce, PPK = Liczba meczów przegranych po karnych, P = Liczba meczów przegranych   Drużyna, która wygra mecz w czasie regulaminowym otrzymuje 3 punkty, zaś drużyna przegrana pozostaje bez punktów. W przypadku, gdy mecz zakończy się remisem następuje dogrywka.  Zespół zwyciężający w dogrywce lub po karnych otrzymuje 2 punkty, a przegrany 1 punkt.   Oblicz, ile punktów zdobyły cztery najlepsze drużyny rundy zasadniczej. Uzupełnij tabelę.    3.      Justyna Kowalczyk na Zimowych Igrzyskach Olimpijskich w Soczi w biegu na 10 km zdobyła złoty medal. Dystans ten pokonała w 28 minut i 17,8 sekund. Czas biegu srebrnej medalistki Charlotte Kalla wyniósł 28 minut i 36,2 sekund. O ile szybciej polska biegaczka pokonywała 1 kilometr niż Charlotte Kalla. Oblicz średni czas.     Kl. V   1.      Boisko do gry w piłkę siatkową        Boisko do gry jest prostokątem o powierzchni 162 m², ograniczonym dwiema liniami końcowymi i dwiema liniami bocznym długości 18 m każda. Oś linii środkowej dzieli boisko na dwa równe pola. Na każdej stronie wyznaczona jest strefa ataku, ograniczona linią środkową, liniami bocznymi i linią ataku znajdującą się 3 m od osi linii środkowej.   Oblicz pole powierzchni ataku jednej strony boiska.     2.      Oto fragment tabeli w pewnym sezonie rozgrywek polskiej ligi piłki nożnej.   Msc. Drużyna M Z R P Pkt 1 Śląsk Wrocław 30 17 5 8   2 Ruch Chorzów 30 16 7 7   3 Legia Warszawa 30 15 8 7   4 Lech Poznań 30 15 7 8   5             6             7             Msc. = lokata w tabeli, M = liczba rozegranych spotkań, Pkt = Liczba zdobytych punktów, Z = Liczba meczów wygranych, R = Liczba meczów remisowych, P = Liczba meczów przegranych Drużyna za wygraną zdobywa 3 punkty, przegrany nie zdobywa żadnego punktu. Remis obu drużynom daje po jednym punkcie.   Oblicz, ile punktów zdobyły cztery najlepsze drużyny sezonu. Uzupełnij tabelę.      3.      Japończyk Noriaki Kasai wynikiem 277,4 punktów zdobył srebrny medal na Zimowych Igrzyskach Olimpijskich w 2014 roku. Złotym medalistą igrzysk w Soczi został Kamil Stoch zdobywając o 1,3 punktu więcej. Ile punktów zdobył Kamil Stoch w drugiej rundzie, jeżeli w pierwszej uzyskał ich 143,4 ?      Kl. IV   1.      Boisko do gry w piłkę ręczną.       Czterdziestometrowy dłuższy bok boiska zwany jest linią boczną, a krótszy - linią końcową. Linia końcowa jest 2 razy krótsza niż linia boczna. Oblicz pole powierzchni całego boiska.      2.      Oto fragment tabeli rundy zasadniczej w pewnym sezonie rozgrywek polskiej piłki koszykowej.   Lp. Drużyna Mecze Mecze wygrane Mecze przegrane Punkty 1. Prokom Gdynia 26 24 2   2. Anwil Włocławek 26 22 4   3. Polpharma  Gdańsk 26 18 8   4. Trefl Sopot 26 17 9   5.           6.             Drużyna zwycięska otrzymuje dwa punkty, a przegrana jeden punkt w klasyfikacji.   Oblicz, ile punktów zdobyły cztery najlepsze drużyny rundy zasadniczej. Uzupełnij tabelę.        3.      Betty Heidler niemiecka lekkoatletka specjalizująca się w rzucie młotem w 2011 roku w niemieckim Halle ustanowiła rekord świata uzyskując wynik 79,42 m. W 2014 roku podczas mityngu w Berlinie nasza mistrzyni Anita Włodarczyk odzyskała rekord świata rzucając młotem o 16 cm dalej. Ile wynosi rekord świata w rzucie młotem kobiet?      SPRZEDAWCA   4.12.2014r. odbyły się ostatnie zajęcia w ramach programu mPotęga. Na spotkaniu gościliśmy sprzedawcę – panią Grażynę Ziółkowską. Nasz gość jest sprzedawcą w sklepie z firankami w Pabianicach. Pani Ziółkowska opowiedziała nam o tym, jak bardzo przydaje jej się matematyka w pracy, głównie podczas mierzenia materiału, liczenia powierzchni materiału wykorzystywanego do różnych firanek oraz liczenia utargu i obliczeń pieniężnych. Pani Grażyna przyniosła do szkoły również próbki materiałów ze swojego sklepu, kasę, metkownicę, frędzle do obszywania oraz wiele innych gadżetów wykorzystywanych w domach do upiększania okien.                  Na zajęcia przybyli też przedstawiciele lokalnej telewizji Pro – MOK, którzy postanowili w swoich informacjach poinformować na temat naszego projektu mieszkańców miasta. Na drugą część zajęć pozostali uczniowie klas IV, którzy po opieką pana Henryka Kurasiewicza rozwiązywali zadania matematyczne związane z pracą sprzedawcy.  Uczniowie wszystkich klas otrzymali też zadania do rozwiązania w domu:     Kl. VI   Oto wybrane produkty z kodem i ceną, które możesz kupić z automatu sprzedającego w naszej szkole.     1.      W automacie sprzedającym umieszczono po10 sztuk każdego     produktu. Oblicz utarg z wymienionych w tabeli produktów.   produkt A27 A35 A41 A43 A45 A47 A56 zostało sztuk w automacie 0 3 3 0 4 6 2     2.  Marek wrzucił do automatu trzy monety o tym samym nominale. Za tę kwotę kupił bułkę z szynką(A23), herbatniki zbożowe(A41) i wodę mineralną(A62), bo na sok(A66) nie wystarczyło pieniędzy. Ile reszty wyrzucił automat?   3.  Krawiec, aby zrealizować zamówienie klienta musi zakupić 3,5 m² tkaniny płaszczowej. W sklepie sprzedawano tkaninę płaszczową w belach o szerokości 1,4 m. Ile zapłaci krawiec za tkaninę, jeżeli 1 metr bieżący kosztuje 40 zł.     Kl. V   Oto wybrane produkty z kodem i ceną, które możesz kupić z automatu sprzedającego w naszej szkole.     1.      Oblicz utarg z wymienionych w tabeli produktów.   produkt A11 A27 A41 A45 A52 A62 sprzedano sztuk 9 10 7 5 8 6   2.  Zosia wrzuciła do automatu złotówkę i dwie monety dwuzłotowe. Za tę kwotę kupiła bułkę z serem(A15), wafelki(A45) i sok w kartoniku(A56). Ile reszty otrzyma Zosia?   3.  Z pięćdziesięciometrowej beli tkaniny podszewkowej sprzedano w sklepie 35 metrów bieżących. Jaka jest wartość pozostałej w beli tkaniny,  jeżeli 1 mb. kosztuje 23 zł?     Kl. IV   Oto wybrane produkty z kodem i ceną, które możesz kupić z automatu sprzedającego w naszej szkole.     1.      Ile reszty wyda automat?     WRZUCONE MONETY ZŁ 5 zł 1 zł 2 zł 2 zł 1 zł 2 zł 2 zł 5 zł 2 zł 2 zł 2 zł WYBRANE PRODUKTY A41 A17 A56 A15 A62 A45 A56 A66 A11 A47 A62 A45 A21 RESZTA ….zł ….gr ….zł ….gr ….zł ….gr ….zł ….gr ….zł ….gr   2. Agnieszka kupiła bułkę drożdżową(A17), wafelek(A47) i sok porzeczkowy(A66). Zapłaciła w automacie najmniejszą liczbą monet. Jakie to monety? Napisz formułę.   3.  Ile mama zapłaci za 2¼ metra bieżącego tkaniny batystowej, jeżeli 1 mb. kosztuje w sklepie 40 zł?     PODSUMOWANIE PROJEKTU          Dzisiejszy dzień, 11.12.2014r, upłynął pod znakiem podsumowań. Najpierw pojechaliśmy na wycieczkę do Experymentarium w Łodzi.  Celem wycieczki było zwiedzenie interaktywnej wystawy – poznawanie zagadnień z różnych dziedzin nauki (magnetyzmu, elektryczności, optyki, dźwięku, mechaniki,  biologii), które stały się proste i czytelne dzięki możliwości wypróbowania ich działania na specjalnych przyrządach oraz na stanowiskach interaktywnych. Niewątpliwą atrakcją była możliwość skorzystania z Tunelu Kosmicznego i udział  w grze tematycznej utrwalającej wiedzę. Nagrodą dla wszystkich był „Certyfikat odkrywcy”.        Po powrocie był czas na rozmowę o poszczególnych zajęciach, ich przydatności oraz statystyka rozwiązań zadań. Wszyscy uczniowie otrzymali  odznaki przedstawiające sprawności lekarza, fotografa, inżyniera, kucharza,  turysty, sportowca, dziennikarza, mistrza igły, sprzedawcy. W zależności od tego, które zadania zostały wykonane najlepiej – taka sprawność została przyznana.                                                 Uczniowie, którzy zdobyli najwięcej punktów, otrzymali też nagrody rzeczowe – torby turystyczne. Te nagrody otrzymali:   Paulina Krajewska klasa Vb – 106 punktów Wojciech Borowski klasa VIb -   105 punktów Michalina Nowak klasa Vb – 103 punkty Aleksandra Janiszewska klasa IVa -  102 punkty Aleksander Koziróg klasa Va – 101 punktów Kacper Więclewski klasa IVa – 100 punktów Jakub Gorządek klasa IVa – 100 punktów     Autorzy projektu: p. Beata Florczak, p. Henryk Kurasiewicz i  p. Janusz Kożlenko